关系代数运算

关系就是一组组由不同属性组成的数据
例如有一组关系组成为 [性别|年龄|名称] 与 [名称|学历]
跨越不同的关系时， 数据往往是离散的。那些离散数据的重新组合与封装我理解为关系代数运算。
这两组独立的关系数据集可以通过重新组合封装成新的数据集。 如 [性别|年龄|名称|学历] ，进行的重新组合封装操作则可以抽象为关系代数的运算

关系代数运算就类似于普通的算数运算, 由运算符与算数构成， 就像

1 + 1 = 2 //1就是算数, 而 + 就是运算符。

关系代数运算也是由关系运算符与关系实例(元组 tuple)构成。 分别有这几种常用的关系操作

并、差、交

并差交运算对于的是相容的关系，即两个关系他们的属性值相同。例如两个关系，都具有属性 [性别|年龄|名称]。

并

并就是将两组关系结合在一起，消去相同的值。用符号 ∪ 表示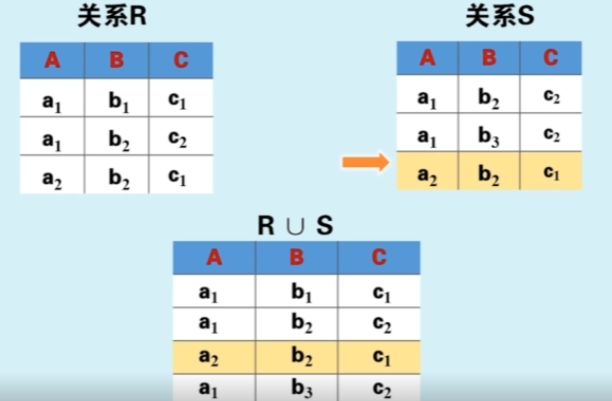

差

差也很好理解， 就是被减数的集合内去掉与减数集合内交叉的部分（哈哈这样我自己感觉比较好理解。 用符号 - 表示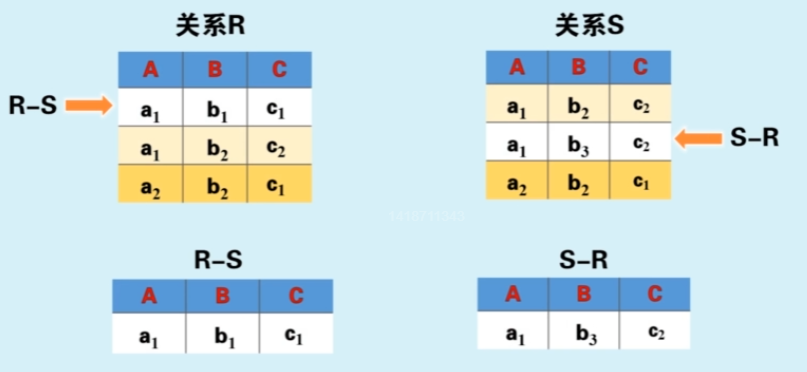

交

交就更好理解了！！就是两个集合中都出现的元组。 用符号 ∩ 表示
图片脑补中(●’◡’●)….

∩ ∪ ∩ 这是交并交, ∩ - ∩ 这是交差交， ∪∩∪ 这是并交并 哈哈

投影、选择

投影

并差交运算是相对于多个关系进行的，而投影则是对于一个关系进行的运算， 投影这词儿可能不太好理解。 我理解成是将关系中某列抽出来， 我称之为出列， 为啥这样说呢， 看示例图就很明了了。

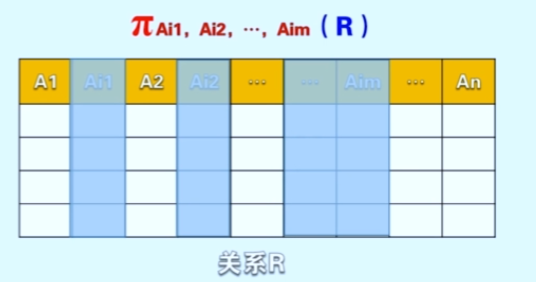
图中将蓝色部分的列都抽出来形成一个新的关系，投影操作用Π(pi)表示,后面的下标则代表要 出列 哪几个关系也就是哪几列，括号里代表的是关系名
投影操作后由于要合并相同的元组， 所以投影的结果元组数可能会减少

选择

如果把投影成为出列， 那选择就是出行了， 把符合条件的某几行抽出来，形成一个新的关系， 该关系是原来关系的子集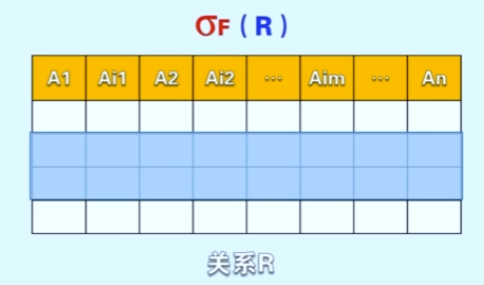

选择操作与条件息息相关。 选择的条件可以为> . < 、= 等。经过条件的过滤则可以选择出想要的元组集合. 用符号σ表示

广义笛卡尔积、连接、重命名

广义笛卡尔积

广义笛卡尔积是两个不同关系之间的运算。相对于将关系的属性拼接后，数据的重新组合。具体操作看下图就很清晰了

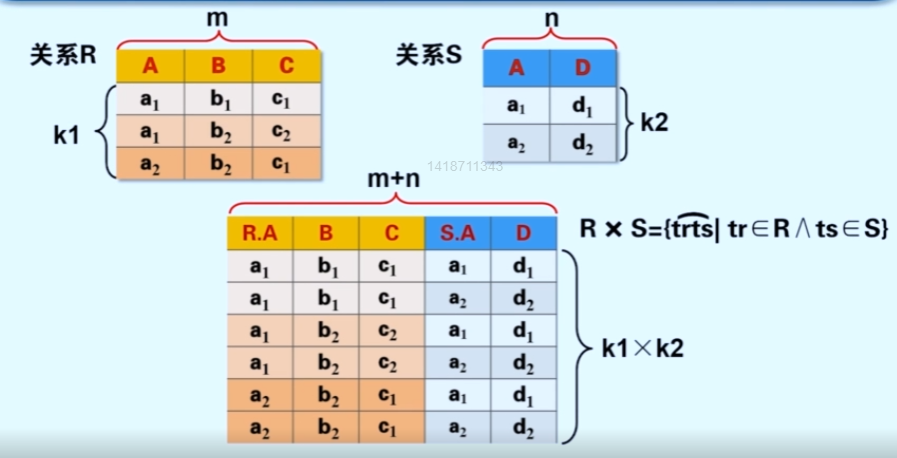
图中下面的那张表就是进行笛卡尔积后的结果， 新关系的属性变成m+n， 新关系的元组变成k1*k2

连接, 重命名

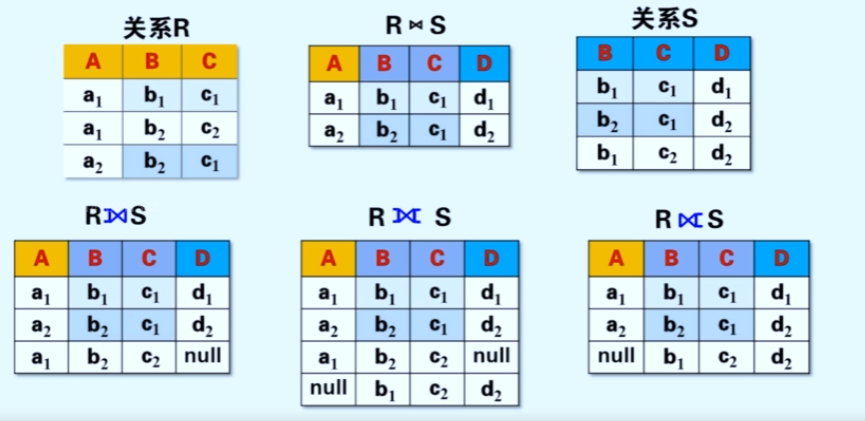
连接操作是基于广义笛卡尔积的结果进行有条件的筛选,有如下几种连接方式

• seta连接的seta代表某一种条件操作. 如关系中的某一个属性满足某个条件.
• 等值连接为seta连接的一种. 指代某个属性值相等, 常用于相关联的两个表对同名属性的连接. 如学生表中的学号与学生选课表中的学号
• 自然连接代表在进行等值连接时去掉了相同属性的连接
• 外连接就是在自然连接的基础上保留因为没有值而造成的悬空情况
  
• 自身连接就是自身内部存在某种自然联系, 可以通过自身某个属性的连接来构造新的关系, 如下图
  
  自身连接还存在关系名重复的问题, 关系本身是S, 不存在S与S的连接. 故需要对关系进行重命名如变成 S(左图)与S’(右图)

除

命令操作

# 可用于shell中压缩图片大小
#!/bin/bash

# Optimize JPEG/JPG files
for img in *.jpg *.jpeg; do
    if [ -f "$img" ]; then
        echo "Optimizing $img"
        jpegoptim --strip-all --all-progressive "$img"
    fi
done

# Optimize PNG files
for img in *.png; do
    if [ -f "$img" ]; then
        echo "Optimizing $img"
        optipng -o7 "$img"
    fi
done

echo "Optimization complete."